En otras palabras, Heissenberg nos da a escoger entre saber muy bien cual es la posición (o sea, poco Δx, error de posición) y desconocer la velocidad (mucho Δv); o conocer muy bien la velocidad y desconocer la posición. Dos pregunta que quizás te hayan surgido:
1º ¿De donde sale v? "p" es el momento, que se define como m·v. La masa es una constante, luego lo que realmente varía (y donde cometemos más error) es en la posición. Luego el Principio de Incertidumbre se podría expresar como:
m · (Δx · Δv) ≥ 1'05 × 10 -34
2º ¿Por qué solo se puede conocer bien una cosa? El producto de los errores es una constante. Luego si soy muy preciso en la posición, hago Δx muy pequeño, obligatoriamente Δv debe aumentar (para que el producto de ambos sea constante). Lo mismo si quiero ser muy preciso en la velocidad.
Este Principio se puede aplicar a todo (como hemos dicho, la Cuántica se puede aplicar a todo). Pero vamos a ver que en unos casos es importante, y en otros se puede despreciar.
Por ejemplo, imagina que un GPS me permite localizar un coche de 1500 Kg con una precisión de 5 m. ¿Cuál es la precisión que me puedo permitir en la velocidad?Δv ≥ ħ / (m · Δx)
Δv ≥ 7 × 10 -39 m/s
Como vemos, el error de la velocidad es muy pequeño, tan pequeño que ni lo notamos.
Ahora pongamos como ejemplo un electrón (m= 9'11 × 10 -31), cuya posición podemos conocerla con una precisión de 0'0000001 m. ¿Cuál es la precisión que me puedo permitir en la velocidad?
Δv ≥ 576'29 m/s
PODEMOS CONOCER LA VELOCIDAD DE CUALQUIER CUERPO CON UNA PRECISIÓN DE 0'005 m/s. ¿CON QUÉ PRECISIÓN PODEMOS CONOCER LA LOCALIZACIÓN DE UNA PELOTA DE 1 Kg Y DE UN PROTÓN (m = 1'67 × 10 -27Kg)? [SOLUCIÓN EN COMENTARIOS]
El error en la velocidad es muy grande, tanto, que no puedo conocer la velocidad.
Recopilemos:
En Cuántica solo podemos conocer bien la posición o la velocidad, pero no las dos
En Mecánica Cuántica debemos tener siempre la duda en mente (sin saber los dos datos, posición y velocidad, bien, no podemos saber la trayectoria). Vamos a trabajar en todo momento con probabilidades, algo que supuso un "shock" para los físicos más ortodoxos que no concebían una Física de incertidumbres. Para la historia queda la frase de Einstein criticando la Mecánica Cuántica:"Dios no juega a los dados"
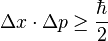
PODEMOS CONOCER LA VELOCIDAD DE CUALQUIER CUERPO CON UNA PRECISIÓN DE 0'005 m/s. ¿CON QUÉ PRECISIÓN PODEMOS CONOCER LA LOCALIZACIÓN DE UNA PELOTA DE 1 Kg Y DE UN PROTÓN (m = 1'67 × 10 -27Kg)?
ResponderEliminarm · (Δx · Δv) ≥ 1'05 × 10 -34
Δv = 0'005 m/s
En el caso de la pelota, Δx = 2'1 · 10^(-32) m
En el caso del protón, Δx = 1'26 · 10^(-5) m
En el caso de la pelota, el error es muy pequeño, luego no podemos aplicarle la Mecánica Cuántica, es decir, podemos saber con bastante precisión su velocidad y su posición.
En el caso del protón, el error es mayor. Luego podemos aplicarle la Cuántica, aunque se encontraría justo en la frontera (o sea, su movimiento tendría características de Cuántica y Clásica).