Ψ = senx Ψ = cosx
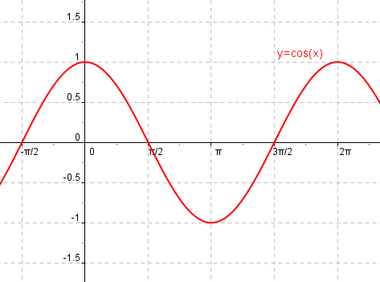
Pero no todas son tan sencillas como esta, más quisieras. Por ejemplo, la del átomo de hidrógeno (el más sencillo de todos los átomos):
Imaginemos que tenemos una partícula que sigue una función de onda de Ψ, y se encuentra "encerrada" en una caja que mide L . ¿Cuál es la probabilidad de encontrar la partícula entre "a" y "b"? Pues se define como:
P (a ≤ x ≤ b) = [∫Ψ·Ψ· dx] entre x=b y x=a
Eso es lo mismo que decir que esa probabilidad es el área de la región comprendida entre la función de onda al cuadrado, Ψ·Ψ, y el intervalo [a,b], o sea, el valor del área de la región amarilla.
Bueno, ¿y la probabilidad de encontrar a la partícula entre 0 y L? Pues si la partícula se encuentra encerrada en una caja, la probabilidad de encontrar a la partícula dentro de la caja debe ser 1 (el 100 %). Pero no siempre es así.
Siempre que nos dan una función de onda, debemos ver si se cumple esto; y si no, debemos normalizarla. No es más que multiplicarla por un número (constante de normalización) que haga que la probabilidad de encontrar a la partícula dentro de la caja sea 1 (y no 2'5 o 0'33, lo cual sería un sinsentido).
La ecuación de Schrödinger (sí, el del gato zombie) nos dice que:
H, es el hamiltoniano, un operador que nos da la energía total del sistema
E, es la energía del estado cuántico que estudiemos
No caigamos en quitar Ψ por estar multiplicando a ambos lados y decir H = E. No es una ecuación, es un problema de autovalores y autovectores, Matemáticas del nivel de primero de carrera, y que solo vamos a nombrar.
Recopilemos:
La función de onda describe ondas
Debe estar normalizada
La función de onda al cuadrado está relacionada con la probabilidad
La búsqueda de esas Ψ es algo muy complicado. Para simplificar el asunto, usamos modelos cuánticos. Algunos de ellos serán estudiados a partir del próximo post. Despedimos el post con un meme del amigo Schrödinger.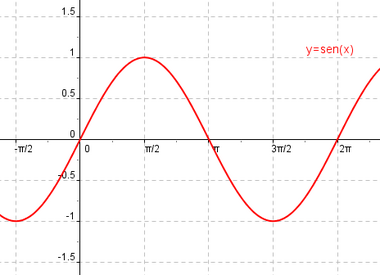
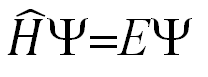
No hay comentarios:
Publicar un comentario